Distributed Energy Resources - Lecture 3: Linear Ordinary Differential Equations

Other notes in this series from Kevin Kircher’s Distributed Energy Resources class are here.

Summary

A lot of derivations for one lecture. Especially given how comparatively light on content the first two lectures were.

See derivations for solutions to general first-order linear scalar ordinary differential equations (ODEs). I have not missed $\text{LATEX}$ and mostly wrote this out to keep me honest in working through the derivations. Probably not a great use of time.

• General first order linear scalar ODE
  • $x(t^{init})=x^{init},\frac{dx(t)}{dt}=a(t)x(t)+b(t)$
  • $\text{has the solution }x(t)=\frac{1}{g(t)}[g(t^{init})x^{init}+{\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau ]$
  • $\text{where }g(t)=e^{-\int a(t)dt}$
• If $a$ is a constant, then:
  • $g(t)=e^{-ta}$
  • $\text{and }x(t)=e^{(t-t^{init})a}{x}^{init}+e^{ta}{\int }_{t^{init}}^t{e}^{-\tau a}b(\tau )d\tau$
• If $b$ is constant and $a\ne 0$, then:
  • $x(t)=e^{(t-t^{init})a}{x}^{init}+\frac{b}{a}(e^{ta-t^{init}}-1)$

Then we derived a simple model of stored chemical energy in a battery:

• Introduced the concept of $\tau$ (h), the self-dissipation time constant - characterises the rate at which a battery loses its stored energy due to internal chemical reactions, even when it’s not connected to an external load. This phenomenon is commonly known as self-discharge. It is the time it takes for the battery’s charge (or voltage, or capacity) to drop to approximately $1/e$ of its initial value due to self-discharge alone.

• Introduced the concept of $p^{chem}(t)$ (kW), the chemical charging power (or discharging if $p^{chem}(t)<0$), the rate at which electrical energy is converted into chemical potential energy within the battery during the charging process. It’s the portion of the input electrical power that is successfully converted and stored as chemical energy within the battery.

• If we assume $\tau$ and $p^{chem}$ are constant, then we get $x(t)=e^{-(t-t^{init})/\tau }{x}^{init}+[1-e^{-(t-t^{init})/\tau }]\tau p^{chem}$

• General first order vector scalar ODE

  • $x(t^{init})=x^{(init)}\in R^n,\frac{dx(t)}{dt}=A(t)x(t)+b(t)$
  • where $A(t)\in R^{n\times n},b(t)\in R^n$ and the variable is $x:R\to R^n$
  • has no analytical solution for general time-varying $A(t)$
  • But for constant A, the IVP has a solution
    • $x(t)=e^{(t-t^{init})A}{x}^{init}+e^{tA}{\int }_{t^{init}}^t{e}^{-\tau A}b(\tau )d\tau$

• If $A$ is invertible and $b$ is constant, then**

  • $x(t)=e^{(t-t^{init})A}{x}^{init}+[e^{(t-t^{init})A}-I]A^{-1}b$

• If $A$ and $b$ are constant, then

  • $x(t)=e^{(t-t^{init})A}{x}^{init}+e^{tA}{\int }_{t^{init}}^t{e}^{-\tau A}d\tau b$

Notes

Homework

Exercise #1

• Consider the IVP (initial value problem) $x(1)=1/2,\frac{dx(t)}{dt}=-\frac{2x(t)}{t}+t-1+1/t$
• write down $a(t)$ and $b(t)$
  • $a(t)=-\frac{2}{t};b(t)=t-1+1/t$
• find $g(t)$
  • $g(t)=e^{-\int a(t)dt}=e^{-\int \frac{-2}{t}dt}=e^{2\int \frac{1}{t}dt}=e^{2\ln |t|}$
  • From $a\ln b=\ln b^a$: $g(t)=e^{\ln t^2}=t^2$
• find ${\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau$
  • ${\int }_{t^{init}}^t{\tau }^2(\tau -1+1/\tau )d\tau ={\int }_{t^{init}}^t({\tau }^3-{\tau }^2+\tau )d\tau$
  • $=(\frac{t^4}{4}-\frac{t^3}{3}+\frac{t^2}{2})-(\frac{{t^{init}}^4}{4}-\frac{{t^{init}}^3}{3}+\frac{{t^{init}}^2}{2})$
  • $=\frac{t^4}{4}-\frac{t^3}{3}+\frac{t^2}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{2})=\frac{t^4}{4}-\frac{t^3}{3}+\frac{t^2}{2}-\frac{5}{12}$
• write down the solution $x(t)$
  • $x(t)=\frac{1}{g(t)}[g(t^{init})x^{init}+{\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau ]$
  • $x(t)=\frac{1}{t^2}[{t^{init}}^2{x}^{init}+\frac{t^4}{4}-\frac{t^3}{3}+\frac{t^2}{2}-\frac{5}{12}]$
  • $x(t)=\frac{1}{2t^2}+\frac{t^2}{4}-\frac{t}{3}+\frac{1}{2}-\frac{5}{12t^2}=\frac{t^2}{4}-\frac{t}{3}+\frac{1}{2}+\frac{1}{12t^2}$

Exercise #2

Prove the linear vector ODE IVP solution:
$x(t^{init})=x^{init}\in \mathbb{R},\frac{dx(t)}{dt}=A(t)x(t)+b(t)$
$\Rightarrow x(t)=e^{(t-t^{init})A}{x}^{init}+e^{tA}{\int }_{t^{init}}^t{e}^{-\tau A}b(\tau )d\tau$

• $x(t^{init})=x^{init}\in \mathbb{R},\frac{dx(t)}{dt}=A(t)x(t)+b(t)$
  • where $A(t)\in R^{n\times n},b(t)\in R^n,x:R\to R^n$
• multiplying by any positive $G:R\to R^{n\times n}$
  • $G(t)\frac{dx(t)}{dt}-G(t)A(t)x(t)=G(t)b(t)$
• recall that for $G:R\to R^{n\times n}$ and $b:R\to R^n$,
  • $\frac{d}{dt}(G(t)x(t))=G(t)\frac{dx(t)}{dt}+\frac{dG(t)}{dt}x(t)$
• $\text{If we assume }\frac{dG(t)}{dt}=-G(t)A(t)\text{, then:}$
  • $\frac{d}{dt}(G(t)x(t))=G(t)\frac{dx(t)}{dt}-G(t)A(t)x(t)$
  • $\frac{d}{dt}(G(t)x(t))=G(t)b(t)$
• Guess $G(t)=e^{-tA}$
• $\frac{dG(t)}{dt}=-A{e}^{tA}=-e^{tA}A=-G(t)A(t)$
• So taking $\frac{d}{dt}(G(t)x(t))=G(t)b(t)$
  • $\Rightarrow {\int }_{t^{init}}^t\frac{d}{d\tau }(G(\tau )x(\tau ))d\tau ={\int }_{t^{init}}^{t}G(\tau )b(\tau )d\tau$
  • $\Rightarrow G(t)x(t)-G(t^{init})x(t^{init})={\int }_{t^{init}}^{t}G(\tau )b(\tau )d\tau$
  • $\Rightarrow x(t)=\frac{1}{G(t)}[G(t^{init})x(t^{init})+{\int }_{t^{init}}^{t}G(\tau )b(\tau )d\tau ]$
  • $\Rightarrow x(t)=e^{tA}[e^{-t^{init}A}x(t^{init})+{\int }_{t^{init}}^t{e}^{-\tau A}b(\tau )d\tau ]$
  • $\Rightarrow x(t)=e^{(t-t^{init})A}{x}^{init}+e^{tA}{\int }_{t^{init}}^t{e}^{-\tau A}b(\tau )d\tau$

---

• A quick refresh on vectors and matrices.
• A chance to practice some $\text{LATEX}$.
• An nth-order ODE is linear if it can be written as $$\frac{d^{n}x(t)}{d{t}^n}=a_{n-1}(t)\frac{d^{n-1}x(t)}{d{t}^{n-1}}+...+a_1(t)\frac{dx(t)}{dt}+a_0(t)x(t)+b(t)$$ for some functions $a_0,...,a_{n-1},b:R\to R$
• So
  • $\frac{dx(t)}{dt}=e^{-t}x(t)-3$ is first-order linear, but would be non-linear if it was $x^2(t)$. The thing that matters for linearity is whether there are non-linear functions of $x$
  • $\frac{d^{2}x(t)}{d{t}^2}=sin(x(t))$ is second-order non-linear because the RHS is not a linear function of $x$
  • $\frac{d^{3}x(t)}{d{t}^3}=t\frac{dx(t)}{dt}-x(t)$ is third-order linear
• ==Derive the general solution to the general first-order linear scalar ODE:==
  • $x(t^{init})=x^{init},\frac{dx(t)}{dt}=a(t)x(t)+b(t)$
  • $\text{multiplying by any positive }g:R\to R\text{ gives:}$ $g(t)\frac{dx(t)}{dt}-x(t)a(t)g(t)=g(t)b(t)$
  • $\text{Recall that }\frac{d}{dt}(x(t)g(t))=\frac{dx(t)}{dt}g(t)+x(t)\frac{dg(t)}{dt}$
  • $\text{So if }\frac{dg(t)}{dt}=-a(t)g(t)\text{, then:}$ $\frac{d}{dt}(x(t)g(t))=g(t)b(t)$
  • Let $\int a(t)dt$ denote an antiderivative of $a$
  • Guess $g(t)=e^{-\int a(t)dt}$ ⇒ this satisfies $g$ as always positive since $e^z>0,z\in R$
  • But does it work?
    • $\frac{dg(t)}{dt}=\frac{d}{dt}{e}^{-\int a(t)dt}$
    • $=e^{-\int a(t)dt}\frac{d}{dt}(-\int a(t)dt)$
    • $=e^{-\int a(t)dt}(-a(t))$
    • $=-a(t)g(t)\text{ which satisfies our requirement}$
  • with $g(t)=e^{-\int a(t)dt}\text{, we have}$ $\frac{d}{dt}(x(t)g(t))=g(t)b(t)$ $\Rightarrow {\int }_{t^{init}}^t\frac{d}{d\tau }(x(\tau )g(\tau ))d\tau ={\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau$
  • $\Rightarrow x(t)g(t)-x(t^{init})g(t^{init})={\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau$
  • $\Rightarrow x(t)=\frac{1}{g(t)}[g(t^{init})x(t^{init})+{\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau ]$
  • General first order linear scalar ODE $x(t^{init})=x^{init},\frac{dx(t)}{dt}=a(t)x(t)+b(t)$ $\text{has the solution }x(t)=\frac{1}{g(t)}[g(t^{init})x^{init}+{\int }_{t^{init}}^{t}g(\tau )b(\tau )d\tau ]$ $\text{where }g(t)=e^{-\int a(t)dt}$
  • If $a$ is a constant, then: $g(t)=e^{-ta}$ $\text{and }x(t)=e^{(t-t^{init})a}{x}^{init}+e^{ta}{\int }_{t^{init}}^t{e}^{-\tau a}b(\tau )d\tau$
  • If $b$ is constant and $a\ne 0$, then: $x(t)=e^{(t-t^{init})a}{x}^{init}+e^{ta}.b{\int }_{t^{init}}^t{e}^{-\tau a}d\tau$ $\text{since }\int e^{-\tau a}d\tau =\frac{-1}{a}{e}^{-\tau a}$ $x(t)=e^{(t-t^{init})a}{x}^{init}+b\frac{e^{ta}}{a}(-e^{-ta}+e^{-t^{init}a})$ $=e^{(t-t^{init})a}{x}^{init}+\frac{b}{a}(e^{ta-t^{init}}-e^{ta-ta})$ $x(t)=e^{(t-t^{init})a}{x}^{init}+\frac{b}{a}(e^{ta-t^{init}}-1)$
• Simple model of a battery is $\frac{dx(t)}{dt}=-\frac{x(t)}{\tau }+p^{chem}(t)$ where:
  • $x(t)\in R$ (kWh) is the stored chemical energy
  • $\tau >0$ (h) is the self-dissipation time constant - characterises the rate at which a battery loses its stored energy due to internal chemical reactions, even when it’s not connected to an external load. This phenomenon is commonly known as self-discharge. We will see shortly that this is the time it takes for the battery’s charge (or voltage, or capacity) to drop to approximately $1/e$ of its initial value due to self-discharge alone.
  • $p^{chem}(t)$ (kW) is the chemical charging power (or discharging if $p^{chem}(t)<0$)
  • This is a first order linear ODE with
    • $a=-\frac{1}{\tau }$ (constant, so we can use one of the simplified solutions.
    • $b=p^{chem}(t)$
  • If $p^{chem}(t)$ is constant, we get $x(t)=e^{-(t-t^{init})/\tau }{x}^{init}+[1-e^{-(t-t^{init})/\tau }]\tau p^{chem}$
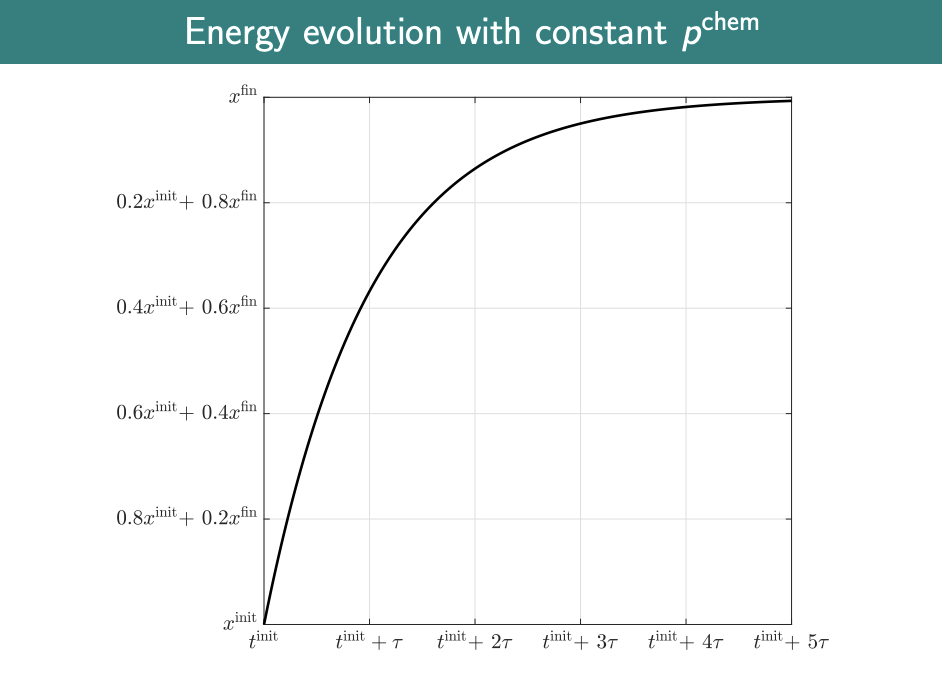
  • As $t\to \infty ,x(t)$ approaches a steady final state $x^{fin}=\tau p^{chem}$
• Can also think of the state of a battery at any time as a mixture of initial and final states:
  • any mixture of quantities $z_1$ and $z_2$ can be written as $\lambda z_1+(1-\lambda )z2$ where $\lambda \in [0,1]$
  • since $\tau$ is positive, $e^{-(t-t^{init})/\tau }\in [0,1]$ for all $t\ge t^{init}$
  • so with constant $p^{chem}$ the battery IVP solution is $x(t)=e^{-(t-t^{init})/\tau }{x}^{init}+[1-e^{-(t-t^{init})/\tau }]x^{fin}$
  • This is a mixture of $x^{init}$ and $x^{fin}$ weighted by $\lambda =$e^{-(t-t^{init})/\tau}$
• Define the normalised gap between $x(t)$ and $x^{fin}$ $y(t)=\frac{x^{fin}-x(t)}{x^{fin}-x^{init}}$ apparently this simplifies to $y(t)=e^{-(t-t^{init})/\tau }$ so after $n$ time constants ($\tau$), $100\times e^{-n}=$ % remaining
• Linear vector ODEs

  • A first-order linear vector ODE has the form $\frac{dx(t)}{dt}=A(t)x(t)+b(t)$ where $A(t)\in R^{n\times n},b(t)\in R^n$ and the variable is $x:R\to R^n$

  • So very like a first-order linear scalar ODE, but replacing $a(t)$ with a square matrix of functions, $b(t)$ and $x(t)$ with a column vectors of functions. It’s a generalisation of the scalar case.

  • Writing it out $\left[\begin{array}{c}d{x}_1(t)/dt\\ ⋮\\ d{x}_n(t)/dt\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}(t)& \dots & A_{1n}(t)\\ ⋮& & ⋮\\ A_{n1}(t)& \dots & A_{nn}(t)\end{array}\right]\left[\begin{array}{c}{x}_1(t)\\ ⋮\\ x_n(t)\end{array}\right]+\left[\begin{array}{c}{b}_1(t)\\ ⋮\\ b_n(t)\end{array}\right]$

  • Consider the nth-order linear scalar ODE $x^{(n)}=a_{n-1}{x}^{n-1}+\cdots +a_1{x}^{(1)}+a_{0}x+b$ with time arguments suppressed and notation $x^{(i)}=\frac{d^{i}x}{d{t}^i}$

  • define a new variable $z:R\to R^n$ by $z=(x,\dots ,x^{(n-1)})$

  • then the first derivative of $z$ is $\left[\begin{array}{c}{x}^{(1)}\\ ⋮\\ x^{(n-1)}\\ x^{(n)}\end{array}\right]=\left[\begin{array}{cccc}& 1& & \\ & & \ddots & \\ & & & 1\\ a_0& \dots & a_{n-2}& a_{n-1}\end{array}\right]\left[\begin{array}{c}x\\ ⋮\\ x^{(n-2)}\\ x^{(n-1)}\end{array}\right]+\left[\begin{array}{c}\\ \\ \\ \\ b\end{array}\right]$

  • This is a first-order linear vector ODE of the form $\frac{dz}{dt}=A(t)z(t)+c(t)$

  • The first-order linear vector ODE IVP $x(t^{init})=x^{(init)}\in R^n,\frac{dx(t)}{dt}=A(t)x(t)+b(t)$ has no analytical solution for general time-varying $A(t)$

  • But for constant A, the IVP has a solution $x(t)=e^{(t-t^{init})A}{x}^{init}+e^{tA}{\int }_{t^{init}}^t{e}^{-\tau A}b(\tau )d\tau$ where $e^M\in R^{n\times n}$ is the matrix exponential of $M\in R^{n\times n}$

    • $M^2=MM,M^3=MMM$ etc
    • $e^M=I+M+\frac{1}{2!}{M}^2+\frac{1}{3!}{M}^3+\dots$

  • why define a matrix exponential? Because for any $t\in \mathbb{R}$ $\frac{d}{dt}{e}^{tM}=\frac{d}{dt}(I+tM+\frac{t^2}{2!}{M}^2+\frac{t^3}{3!}{M}^3+\dots )$ $=M+t{M}^2+\frac{1}{2!}{t}^2{M}^3+\dots$ $=M(I+tM+\frac{1}{2!}{t}^2{M}^2+\dots )$ $=M{e}^{tM}$ ie: $\frac{d}{dt}{e}^{tM}=M{e}^{tM}=e^{tM}M\text{ for any }t\in \mathbb{R}$

  • $e^0=I$ (where $0$ and $I$ are $n\times n$)

  • $e^{(t_1+t_2)M}=e^{t_{1}M}{e}^{t_{2}M}\text{ for any}{t}_1,t_2\in \mathbb{R}$

  • $e^M$ is always invertible and $(e^{tM}{)}^{-}1=e^{-tM}$: $e^{tM}{e}^{-tM}=e^{(t-t)M}=e^{0M}=e^0=I$

  • if $M$ is invertible, then ${\int }_{t_1}^{t_2}{e}^{tM}dt=M^{-}1(e^{t_{2}M}-e^{t_{1}M})=(e^{t_{2}M}-e^{t_{1}M})M^{-}1$

  • If $A$ is invertible and $b$ is constant, then $x(t)=e^{(t-t^{init})A}{x}^{init}+[e^{(t-t^{init})A}-I]A^{-1}b$

  • If $A$ and $b$ are constant, then $x(t)=e^{(t-t^{init})A}{x}^{init}+e^{tA}{\int }_{t^{init}}^t{e}^{-\tau A}d\tau b$