Distributed Energy Resources - Lecture 6: Buildings, part 1

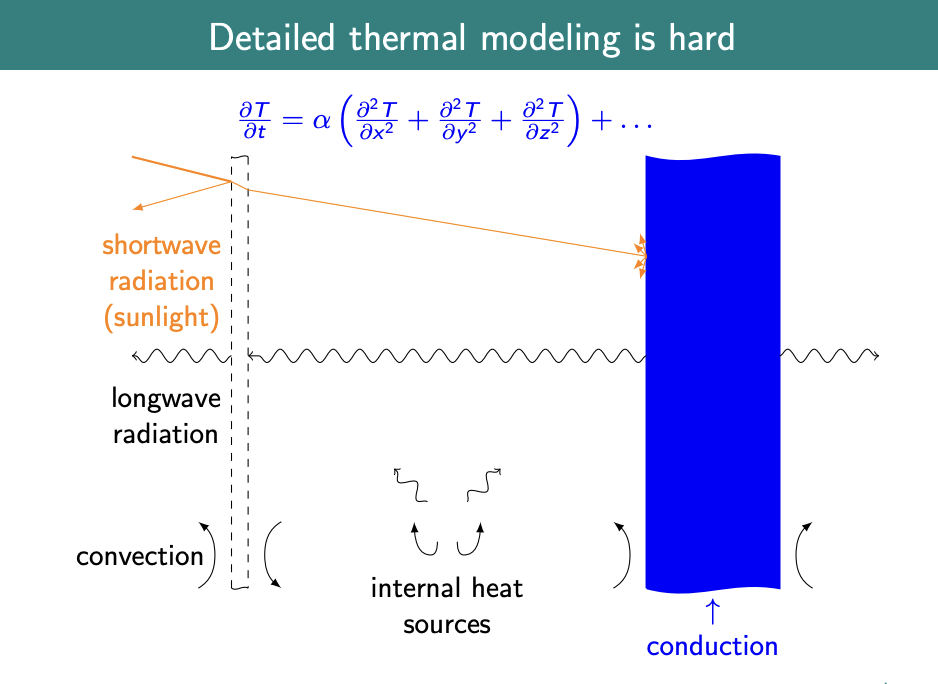
Other notes in this series from Kevin Kircher’s Distributed Energy Resources class are here.

Summary

It turns out that you can reason about building heating/cooling with something called “thermal circuits” that are analogous to electrical circuits. This allows us to reuse things like Ohm’s law and Kirchoff’s laws to reason about heat flow, thermal capacity and insulation (or thermal resistance) in single and connected rooms.

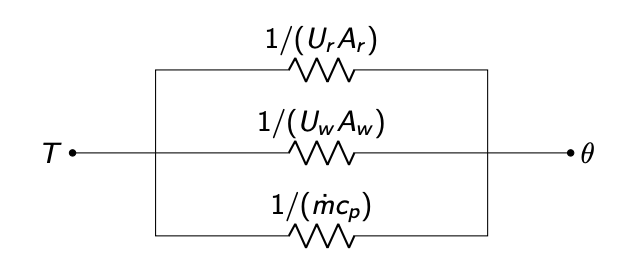
Example: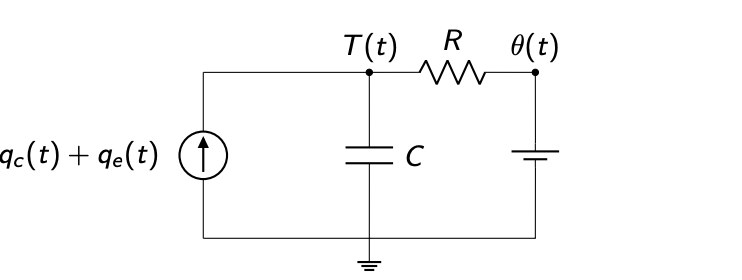

Notes

• buildings = commercial + residential ~ 2/3 of electricity usage in the US
• peaks are typically driven by building aircon on hot days
  • seems like a good argument for distributed generation
• 
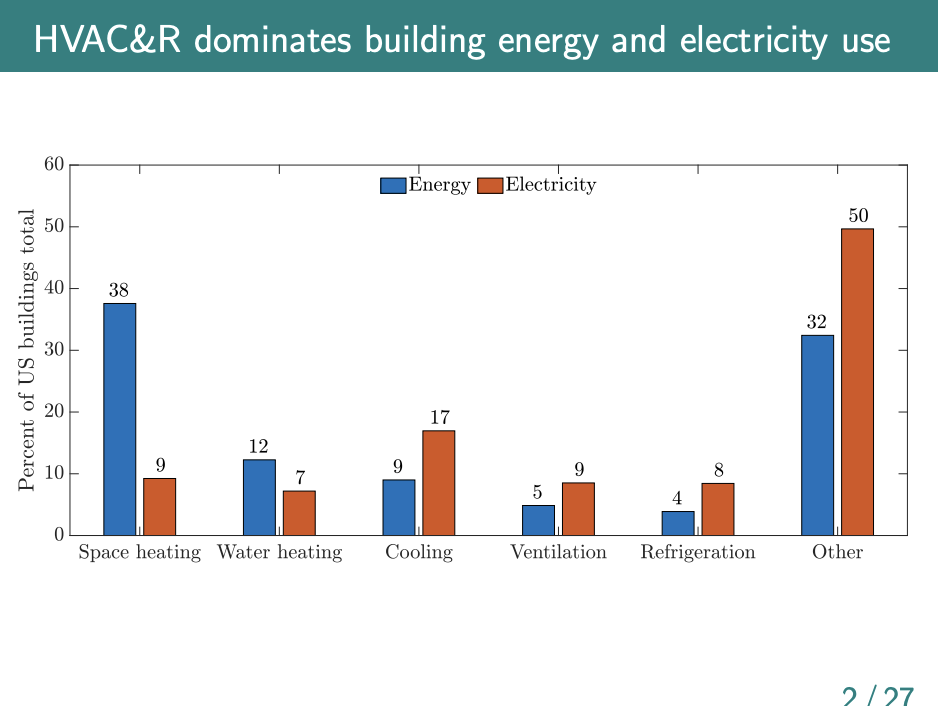
  • y-axis is % of energy used in residential/commercial buildings
  • blue includes electricity
• Simple building energy model
• Thermal circuits are analogous to electrical circuits
  • temperature ↔ voltage - temperature differences drive heat flows
  • heat ↔ charge
  • thermal resistance ↔ electrical resistance
  • thermal capacitance ↔ electrical capacitance
• 1R1C circuit:
  • $T(t)$ is indoor temp
  • $\theta (t)$ is boundary (often outdoor) temp
  • $R{(}^{\circ }C/kW)$ is thermal resistance between $T$ and $\theta$
  • $C(kWh{/}^{\circ }C$ ) is indoor thermal capacitance
  • $q_c(t)(kW)$ is thermal power from controlled equipment
  • $q_e(t)(kW)$ is thermal power from exogenous sources
• So then we can have analogous equation’s to ohm’s law etc
  • Ohm’s law: current through $R$ = $(T(t)-\theta (t))/R$
  • Rate of charge accumulation on $C$ = $CdT(t)/dt$
  • Kirchoff’s current law (KCL) at node $T(t)$:
    • current inflow = current outflow
    • $q_c(t)+q_e(t)=\frac{T(t)-\theta (t)}{R}+\frac{CdT(t)}{dt}$
    • $\Rightarrow \frac{dT(t)}{dt}=\frac{1}{RC}[R(q_c(t)+q_e(t))-T(t)+\theta (t)]$ - First order differential equation, similar to battery formula
    • with a uniform step time $\Delta t$ and piecewise constant $\theta ,q_c,q_e$
    • $T(k+1)=aT(k)+(1-a)R(q_c(k)+w(k))$
      • $a=e^{-\Delta t/RC}$
      • $w(k)=q_e(k)+\theta (k)/R$
• 2R1C
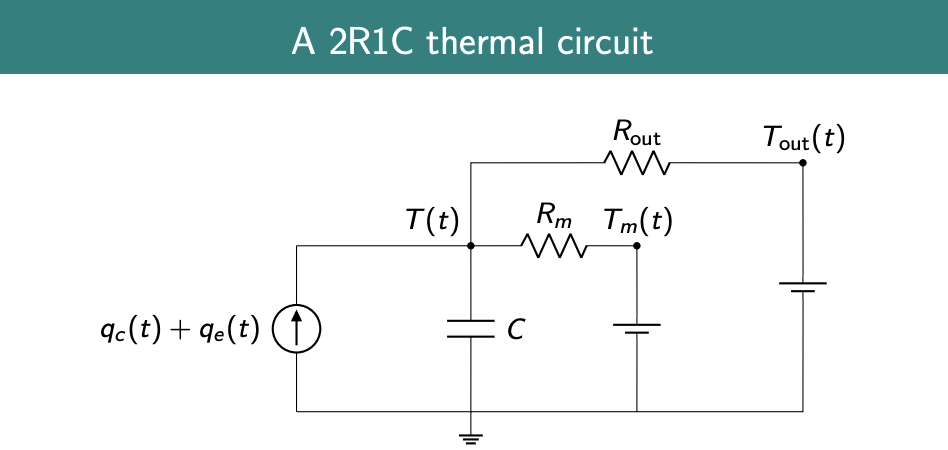
  • $T_m(t)$ is average temperature of thermal mass temperature (walls, etc)
  • $C\frac{dT(t)}{dt}=\frac{T_m(t)-T(t)}{R_m}+\frac{T_{out}-T(t)}{R_{out}}+q_c(t)+q_e(t)$
• nr1C
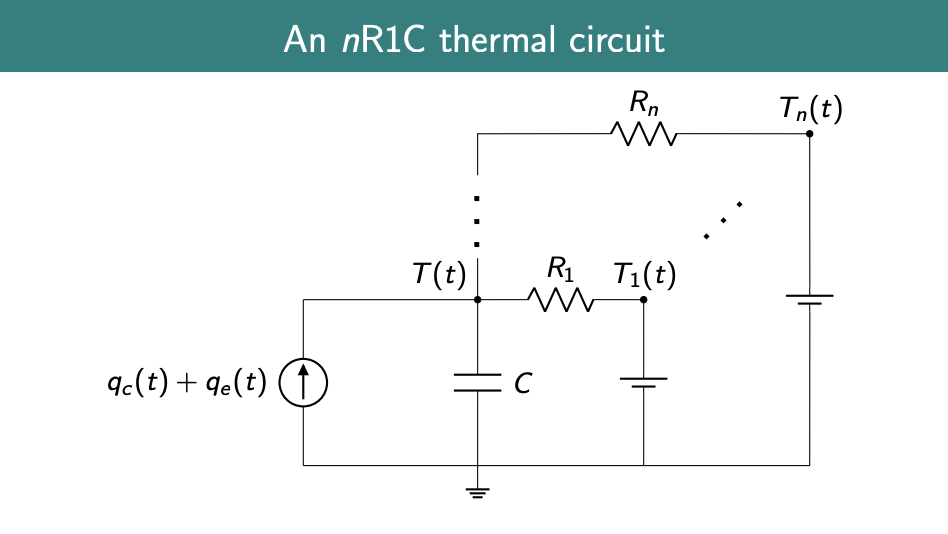
  • physically, parallel resistances represent adjoining rooms (including above and below), and serial resistances the different materials in a barrier between rooms.
  • KCL $\Rightarrow C\frac{dT(t)}{dT}={\sum }_{i=1}^n\frac{T_i(t)-T(t)}{R_i}+q_c(t)+q_e(t)$
  • Parameters
    • Thermal capacitance (C) values for a room it is typically not enough to just look at the air. Other things in the room (furniture, wall decorations, flooring etc) usually have significantly higher thermal capacity than air. Typically multiply the naive, air-only thermal capacitance by 10-15x.
    • Thermal resistance
      • Step 1: get typical heating temperature setpoint $\hat{T}$ (eg: thermostat setting)
      • Step 2: estimate indoor-outdoor temp diff $\delta$ where $q_c$ is zero (typically $6-10^{\circ }$, seems like we could just measure this though)
      • Step 3: define heating balance outdoor temp ${\theta }_h=\hat{T}-\delta$
      • Step 4: get historical $HDD({\theta }_h)$ (heating degree day, ${}^{\circ }C\times$day) over a heating period
      • Step 6: estimate heater efficiency $\eta$
      • Step 7: set $R\approx (\frac{24h}{1day})\frac{HDD({\theta }_h)}{\eta E}$
    • Thermal resistance from first principles
      • 
      • $R=1/(U_r{A}_r+U_w{A}_w\dot{m}{c}_p)$
        • $U$ is thermal transmittance
        • $A$ is outward-facing surface area
        • Subscript $r$ means roof, $w$ means wall/window assemblies
        • $\dot{m}$ is the mass flow rate of outdoor air infiltration
        • $c_p$ is the specific heat of air at pressure $p$
      • For a wall assembly
        • $U_w=\lambda U_{window}+(1-\lambda )U_{wall}$ where $\lambda$ is the fraction of the assembly area that is window.
      • Wall area (for shoebox building), $A_w\approx 4h\sqrt{N{A}_f}$, where $h$ is the floor thickness, N is the number of floors and $A_f$ is floor area.
      • $\dot{m}$ can be estimated based on room volume and desired rate at which air volume is replaced (typically 0.3-0.9 per hour) $1/R\approx (2-5\times 10^{-4}kW/{[}^{\circ }C{m}^2])A_f/N+$
        $(2.8-5.2\times 10^{-3}kW/{[}^{\circ }C{m}^2]h\sqrt{N{A}_f}+$
        $(1.5-2.9+\times 10^{-4}kW/{[}^{\circ }C{m}^3])A_{f}h$
    • Thermal power from sunlight through windows
      • $q_{sun}(t)\approx (1.5-1.7\sqrt{kW}/m)c\lambda h\sqrt{N{A}_f{S}_{tot}^{-}}$
        • $S_{tot}^{-}(kW/m^2)$ is the total solar irradiance on a horizontal surface
        • $c\in [0,1]$ (typically 0.25-0.8) is the solar heat gain coefficient, the fraction of incident solar irradiance that a window transmits